Độ phức tạp thuật toán – Cách tính và ví dụ dễ hiểu cho người mới bắt đầu

Độ phức tạp thuật toán – Cách tính và ví dụ dễ hiểu cho người mới bắt đầu

Mục lục

1. Giới thiệu về độ phức tạp thuật toán


Khi lập trình, đặc biệt là trong cấu trúc dữ liệu và giải thuật, việc chọn thuật toán tối ưu là yếu tố then chốt quyết định tốc độ chạy của chương trình.

Khái niệm độ phức tạp thuật toán (Algorithm Complexity) giúp lập trình viên đo lường và so sánh mức hiệu quả giữa các thuật toán.

Hiểu rõ và biết cách tính độ phức tạp giúp bạn:

  1. Viết chương trình chạy nhanh hơn.
  2. Tiết kiệm tài nguyên máy chủ.
  3. Tránh những lỗi hiệu năng khi website hoặc ứng dụng có nhiều người dùng.


2. Độ phức tạp thuật toán là gì?


Độ phức tạp thuật toán là cách đo lượng tài nguyên (thời gian, bộ nhớ) mà một thuật toán cần để xử lý một bài toán, thường dựa vào kích thước dữ liệu đầu vào (n).


Có hai loại chính:

  1. Độ phức tạp thời gian (Time Complexity) → đo số bước lệnh cần thực hiện.
  2. Độ phức tạp không gian (Space Complexity) → đo dung lượng bộ nhớ cần dùng.


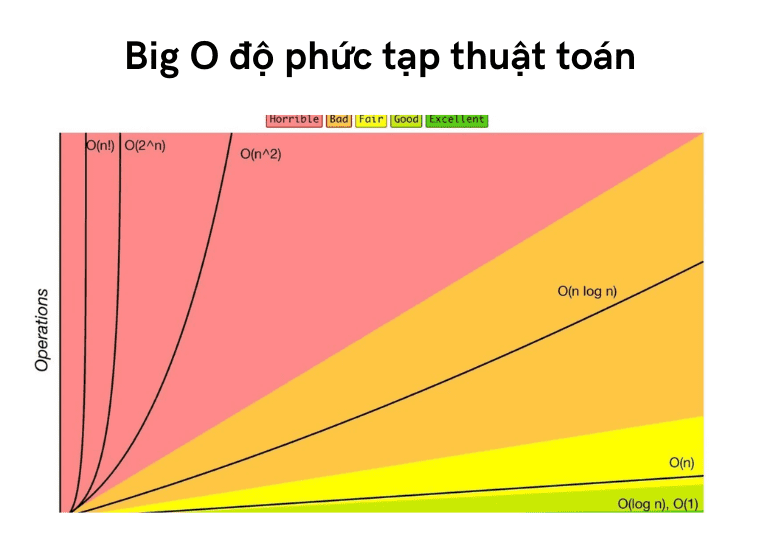
3. Big-O notation – Ngôn ngữ để mô tả độ phức tạp


Để diễn tả độ phức tạp, lập trình viên dùng Big-O notation.

Một số ký hiệu phổ biến:

  1. O(1) → thời gian hằng số (nhanh nhất)
  2. O(log n) → thời gian logarit
  3. O(n) → thời gian tuyến tính
  4. O(n log n) → thời gian tuyến tính nhân logarit
  5. O(n²) → thời gian bậc hai (chậm khi n lớn)
  6. O(2ⁿ) → thời gian hàm mũ (rất chậm)


Ví dụ:

// O(1)
function getFirstElement(arr) {
return arr[0];
}

// O(n)
function printAll(arr) {
for (let i = 0; i < arr.length; i++) {
console.log(arr[i]);
}
}


4. Cách tính độ phức tạp thuật toán


Để tính, ta làm 3 bước:

  1. Xác định các thao tác quan trọng trong thuật toán (thường là vòng lặp, đệ quy, phép toán trên mảng).
  2. Tính số lần lặp hoặc số bước lệnh khi kích thước dữ liệu là n.
  3. Chuyển về dạng Big-O bằng cách bỏ bớt các hằng số và giữ lại thành phần tăng nhanh nhất.


Ví dụ:

// Tính tổng phần tử mảng - O(n)
function sumArray(arr) {
let sum = 0; // O(1)
for (let i = 0; i < arr.length; i++) { // chạy n lần
sum += arr[i]; // O(1) mỗi lần
}
return sum; // O(1)
}
// => Tổng cộng: O(1 + n*1 + 1) ≈ O(n)


5. Bảng so sánh tốc độ tăng trưởng

Big-On=10n=100n=1000
O(1)111
O(log n)3710
O(n)101001000
O(n log n)3070010000
O(n²)10010,0001,000,000


6. Tại sao web developer nên quan tâm?


Trong thiết kế website, việc hiểu và tối ưu độ phức tạp thuật toán giúp:


  1. Tối ưu tốc độ load trang (ví dụ: xử lý dữ liệu JSON lớn).
  2. Cải thiện hiệu năng API.
  3. Giảm chi phí server khi xử lý nhiều request.


Ví dụ: Nếu bạn viết một hàm tìm kiếm sản phẩm trên website:


  1. Thuật toán tìm kiếm tuyến tính (O(n)) có thể chậm khi có hàng chục ngàn sản phẩm.
  2. Dùng Binary Search (O(log n)) sẽ nhanh hơn rất nhiều.


7. Kết luận


Hiểu và tính độ phức tạp thuật toán không chỉ dành cho dân khoa học máy tính, mà cả lập trình viên web cũng cần.

Đây là nền tảng để viết code nhanh hơn – gọn hơn – tiết kiệm hơn.


Từ khóa SEO đề xuất:

độ phức tạp thuật toán, cách tính độ phức tạp thuật toán, big o notation, tối ưu thuật toán, time complexity.

FAQ - Câu hỏi thường gặp

  • 1. Độ phức tạp thuật toán là gì?

    Độ phức tạp thuật toán là thước đo cho biết một thuật toán chạy nhanh hay chậm, tốn nhiều hay ít bộ nhớ khi xử lý dữ liệu. Thông thường, lập trình viên quan tâm nhất đến độ phức tạp thời gian (Time Complexity).

  • 2. Tại sao cần quan tâm đến độ phức tạp thuật toán?

    Nếu không tối ưu, chương trình của bạn có thể chạy rất chậm khi dữ liệu lớn. Ví dụ: một thuật toán O(n²) có thể chạy tốt với 100 phần tử, nhưng sẽ cực kỳ chậm với 100.000 phần tử. Tối ưu thuật toán giúp tiết kiệm thời gian, chi phí và tăng trải nghiệm người dùng.

  • 3. Big-O notation là gì?

    Big-O là cách viết ngắn gọn để mô tả tốc độ tăng trưởng của thuật toán theo kích thước đầu vào.

  • 4. Làm sao để tính độ phức tạp thuật toán?

    Xác định thao tác chính (ví dụ: vòng lặp, đệ quy). Đếm số lần thao tác chạy theo n. Đơn giản hóa về dạng Big-O (bỏ hằng số, chỉ giữ phần tăng nhanh nhất).

Được viết bởi: Ngọc Ngô

Bài viết cùng chuyên mục

Vote 6